Just marked Q12 of Maths Ext1 and have some feedback on Q12e)i)
The question asked students to prove a given vector relationship between A, B and P given that
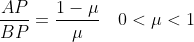
A very common response from students was to assert that
\overrightarrow{BP})
This is
not correct because the given ratio above is purely related to vector magnitudes. To convert to vector equations, you need to take into consideration both the magnitude AND the
direction of the vectors. Notice that vector AP does NOT point into the same direction as BP (as P lies in the interval AB) so they cannot be related by a positive scalar. Many students attempted to fudge the result when they realised the algebra did not work out from this assertion. Better responses carefully considered the directions that the vectors were pointing and often related the directions of AP and AB.

