HSC 2015 MX2 Marathon ADVANCED (archive) (1 Viewer)

Drsoccerball · Jan 25, 2015

Re: HSC 2015 4U Marathon - Advanced Level

when you inverse something doesnt the inequality flip why didnt you flip it for this one?

Sy123 · Jan 25, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Drsoccerball said:
when you inverse something doesnt the inequality flip why didnt you flip it for this one?

Oh right that's a typo, the inequality is flipped after that line

seanieg89 · Jan 25, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Great solution to the first one, very efficient.

Will read the second one a little more carefully later, but it sounds like it is probably right.

My method was to expand

$\sum_{j}(x_{j}-x_{\sigma(j)})(y_{j}-y_{\sigma(j)})\geq 0$

after deducing each individual summand is non-negative from the assumptions.)

seanieg89 · Jan 25, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Interesting that you find the rearrangement inequality harder than the other one! Complete opposite to me.

Sy123 · Jan 26, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Here is something I made:

$\\ $Find$ \ \sum_{n=1}^{\infty} \cos \left(\frac{1}{2}n \right) \cos \left(\frac{3}{2}n \right)$

dan964 · Jan 26, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Latex seems to be playing up on IE10
It was working fine a day ago.

Working fine 9.55am 27th Jan

Sy123 · Jan 26, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Yes my most recent post with a new question won't load the LaTeX for me either, but earlier posts work just fine

$text$

FrankXie · Jan 27, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Sy123 said:
Here is something I made:

$\\ $Find$ \ \sum_{n=1}^{\infty} \cos \left(\frac{1}{2}n \right) \cos \left(\frac{3}{2}n \right)$

can you double check you really meant this one?
$if the series does converge, the limit $ \lim_{n\rightarrow\infty}\cos\frac{n}{2}\cos\frac{3n}{2} $ should be zero, but which i don't think has a limit.$

dan964 · Jan 27, 2015

Re: HSC 2015 4U Marathon - Advanced Level

seanieg89 said:
Great solution to the first one, very efficient.

Will read the second one a little more carefully later, but it sounds like it is probably right.

My method was to expand

$\sum_{j}(x_{j}-x_{\sigma(j)})(y_{j}-y_{\sigma(j)})\geq 0$

after deducing each individual summand is non-negative from the assumptions.)

How would you expand that?

Sy123 · Jan 27, 2015

Re: HSC 2015 4U Marathon - Advanced Level

FrankXie said:
can you double check you really meant this one?
$if the series does converge, the limit $ \lim_{n\rightarrow\infty}\cos\frac{n}{2}\cos\frac{3n}{2} $ should be zero, but which i don't think has a limit.$

I used

$Re\left(\sum_{n=1}^{\infty} (\cos x + i\sin x)^n \right)$ and did stuff with it, I think you can see what I attempted, did I do anything wrong since I'm getting definite finite answers?

hypermax · Jan 27, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Sy123 said:
I used

$Re\left(\sum_{n=1}^{\infty} (\cos x + i\sin x)^n \right)$ and did stuff with it, I think you can see what I attempted, did I do anything wrong since I'm getting definite finite answers?

I've always wanted to study high level maths as a hobby, but where do i begin. When i see these posts I wonder where did you guys start, what textbook did you use.

seanieg89 · Jan 28, 2015

Re: HSC 2015 4U Marathon - Advanced Level

dan964 said:
How would you expand that?

Apologies, the method I had in mind does not quite work when you follow it through.

It is still quite an easy problem though.

1. Observe that the problem is trivial for n=2, with equality iff one of the sequences is constant.

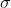
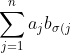2. Suppose $\sigma$ is such that $\sum_{j=1}^n a_jb_{\sigma(j)}$ is maximised.

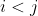
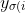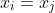
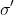
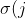3. Suppose there is a pair $i<j$ with $y_{\sigma(i)}>y_{\sigma(j)}$ . Unless $x_i=x_j$ , the permutation $\sigma'$ which agrees with sigma except at i and j, and sends i and j to $\sigma(j),\sigma(i)$ respectively makes the sum strictly larger (contradicting maximality).

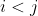
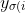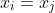
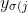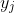
4. So if the sum is maximal then for every pair $i<j$ with $y_{\sigma(i)}>y_{\sigma(j)}$ , we have $x_i=x_j$ . We can then perform the interchange in (3) pairwise without changing the sum, until we have the $y_{\sigma(j)}$ increasing and hence equal to $y_j$ . This completes the proof.

Chlee1998 · Jan 28, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Sy123 said:
I usRe\left(\sum_{n=1}^{\infty} (\cos x + i\sin x)^n \right) [/tex] and did stuff with it, I think you can see what I attempted, did I do anything wrong since I'm getting definite finite answers?

is cisx between plus minus 1? If u used limiting sum

InteGrand · Jan 28, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Isn't the real part of that series going to be $\cos x + \cos 2x + \cos 3x + \cdots$ , which doesn't look like it converges, unless we use other methods of summation (e.g. when $x = \pi$ , Cesàro summation gives $-\frac{1}{2}$ ).

Drsoccerball · Jan 29, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Chlee1998 said:
is cisx between plus minus 1? If u used limiting sum

cis x consists of imaginary and real parts unless x is 0,90,180,270,360....

seanieg89 · Jan 30, 2015

Re: HSC 2015 4U Marathon - Advanced Level

$Given that \\$p(z)=z^3+az^2+bz+c$\\ has all roots on the unit circle, show that \\$q(z)=z^3+|a|z^2+|b|z+|c|$ \\ also has all roots on the unit circle.$

Chlee1998 · Jan 30, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Drsoccerball said:
cis x consists of imaginary and real parts unless x is 0,90,180,270,360....

Which is my point that he cant use the limiting sum formula...

dan964 · Feb 1, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Two comments
I rearranged the original question
To get
1/2 x Lim cos(n) + cos(2n)
Go figure

And secondly its not 90 its pi. You are dealing here with real numbers so use radians. 360 degree = 2 pi

dan964 · Feb 1, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Edit: Pi/2

dan964 · Feb 1, 2015

Re: HSC 2015 4U Marathon - Advanced Level

Next:
For 2015er's

1. Show that if w = 1/x + x
Then w^2 - 2 =x^2 + 1/x^2

2. Use part 1 to show that x^4+....+x+1 = x^2*(w^2+w+1)
And hence factorise the x^4+x^3+...+x+1

3. Solve x^5=1

4. Hence deduce using all parts above to find an exact value for cos (pi/5)) and cos (2pi/5)

5. Repeat the process this time expressing x and w in mod arg form.

Make a Difference – Donate to Bored of Studies!

HSC 2015 MX2 Marathon ADVANCED (archive) (1 Viewer)

Well-Known Member

This too shall pass

Well-Known Member

Well-Known Member

This too shall pass

what

This too shall pass

Active Member

what

This too shall pass

Active Member

Well-Known Member

Member

Well-Known Member

Well-Known Member

Well-Known Member

Member

what

what

what

Users Who Are Viewing This Thread (Users: 0, Guests: 1)