-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Math help (1 Viewer)
- Thread starter Fawun
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)


Re: Math help (Because Carrot made me do this)
Thanks carrot but for part L, how did you get the answer? I don't get how you went from 4^n-2 x 3 blah blah to 1 over 4 x 3^4
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)


Re: Math help (Because Carrot made me do this)
For the denominator for the first one, it's only 4^n-1 x 3^n+2 so how come in the second one, you have 4 x 4^n-2 x 3^n-2 x 3^4? like how come the 4^n-2 and 3^n-2 came out of nowhere?
Also for part g, the answer is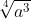
idgi.
For the denominator for the first one, it's only 4^n-1 x 3^n+2 so how come in the second one, you have 4 x 4^n-2 x 3^n-2 x 3^4? like how come the 4^n-2 and 3^n-2 came out of nowhere?
Also for part g, the answer is
Re: Math help (Because Carrot made me do this)
Carrot forgot to simplify. For l, 4^n-2 times 4 equals 4^n-1 (n - 2 + 1 = n - 1, the one from 4^1), its rearranged in order to allow for simplification. Similarily, carrot has broken 3^n+2 into 3^n-2 x 3^4 (n - 2 + 4 = n - 2).idgi.
For the denominator for the first one, it's only 4^n-1 x 3^n+2 so how come in the second one, you have 4 x 4^n-2 x 3^n-2 x 3^4? like how come the 4^n-2 and 3^n-2 came out of nowhere?
Also for part g, the answer is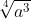
Last edited:
Re: Math help (Because Carrot made me do this)
New question that I need help with:
A lake has an initial pollution of 2 grams/cm^3. Everyday a river flows in a large amount of water of low pollution, and the same amount of water flows out to another river so that the amount of pollution (in gram/cm^3) in the lake at any day t is given by Q = 0.4 + Be^-0.02t
How long will it take to reduce the pollution level to 1 gram/cm^3?
New question that I need help with:
A lake has an initial pollution of 2 grams/cm^3. Everyday a river flows in a large amount of water of low pollution, and the same amount of water flows out to another river so that the amount of pollution (in gram/cm^3) in the lake at any day t is given by Q = 0.4 + Be^-0.02t
How long will it take to reduce the pollution level to 1 gram/cm^3?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
Substitute t=0, Q=2, to find B.
2 = 0.4+Be^0
2 = 0.4+B
B=1.6
So therefore Q = 0.4 + 1.6e^-0.02t
We want the level to be 1, which means Q=1.
1 = 0.4 + 1.6e^-0.02t
0.6 = 1.6e^-0.02t
e^-0.02t = 3/8
-0.02t = ln(3/8)
t = -ln(3/8) / 0.02
t ~ 49.04
Substitute t=0, Q=2, to find B.
2 = 0.4+Be^0
2 = 0.4+B
B=1.6
So therefore Q = 0.4 + 1.6e^-0.02t
We want the level to be 1, which means Q=1.
1 = 0.4 + 1.6e^-0.02t
0.6 = 1.6e^-0.02t
e^-0.02t = 3/8
-0.02t = ln(3/8)
t = -ln(3/8) / 0.02
t ~ 49.04
Re: Math help (Because Carrot made me do this)
Okay I got it thanks. Quick question, I don't get the relationship between log natural and normal logs lol. Like how do you change ln to log form? idgi.Substitute t=0, Q=2, to find B.
2 = 0.4+Be^0
2 = 0.4+B
B=1.6
So therefore Q = 0.4 + 1.6e^-0.02t
We want the level to be 1, which means Q=1.
1 = 0.4 + 1.6e^-0.02t
0.6 = 1.6e^-0.02t
e^-0.02t = 3/8
-0.02t = ln(3/8)
t = -ln(3/8) / 0.02
t ~ 49.04
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
You need to use the change of base law. Natural log is base e but 'normal log' is (I assume) base 10.
So ln = log_e whereas log (just by itself) is assumed to be log_10.
Not sure why you would want to change ln to log_10 since generally problems use ln as opposed to log_10.
But anyway to change it to base 10, we would do this:
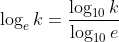
You need to use the change of base law. Natural log is base e but 'normal log' is (I assume) base 10.
So ln = log_e whereas log (just by itself) is assumed to be log_10.
Not sure why you would want to change ln to log_10 since generally problems use ln as opposed to log_10.
But anyway to change it to base 10, we would do this:
Re: Math help (Because Carrot made me do this)
ln(x^2+1)=e ?
Do I expand it?
and what about evaluating without using a calculator:
e^ln 4+ ln 7?
do I have to change anything to log form lol
Oh. So how would you go abouts in solving for x?You need to use the change of base law. Natural log is base e but 'normal log' is (I assume) base 10.
So ln = log_e whereas log (just by itself) is assumed to be log_10.
Not sure why you would want to change ln to log_10 since generally problems use ln as opposed to log_10.
But anyway to change it to base 10, we would do this:
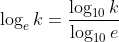
ln(x^2+1)=e ?
Do I expand it?
and what about evaluating without using a calculator:
e^ln 4+ ln 7?
do I have to change anything to log form lol
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
ln(x^2+1) = e = ln(1) (we do this so we can equate the inside)
x^2+1 = 1
x^2 = 0
x = 0.
Remember that e and ln are inverses of each other, so they 'cancel' each other out (function composition etc).
So e^ln(k) = k for any real k.
So therefore e^ln(4) = 4
So the final answer is 4 + ln(7).
ln(x^2+1) = e = ln(1) (we do this so we can equate the inside)
x^2+1 = 1
x^2 = 0
x = 0.
Remember that e and ln are inverses of each other, so they 'cancel' each other out (function composition etc).
So e^ln(k) = k for any real k.
So therefore e^ln(4) = 4
So the final answer is 4 + ln(7).
Re: Math help (Because Carrot made me do this)
So whenever there is an ln and a e in a question, I can just cancel each other out?
So for this question,
ln2e^4 - lne^3, I can just cancel the ln and the e out? elaborate pls.
wat.ln(x^2+1) = e = ln(1) (we do this so we can equate the inside)
x^2+1 = 1
x^2 = 0
x = 0.
Remember that e and ln are inverses of each other, so they 'cancel' each other out (function composition etc).
So e^ln(k) = k for any real k.
So therefore e^ln(4) = 4
So the final answer is 4 + ln(7).
So whenever there is an ln and a e in a question, I can just cancel each other out?
So for this question,
ln2e^4 - lne^3, I can just cancel the ln and the e out? elaborate pls.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
For example:
} = k)
And
 = k)
But if I had:
)
It does NOT equal 2.
So for yor example ln2e^4 - lne^3:
ln(e^3) = 3 because there's nothing else.
But ln(2e^4) has to be changed to ln(2) + ln(e^4) = ln(2) + 4.
They ONLY cancel each other out if there's nothing else except e and ln.wat.
So whenever there is an ln and a e in a question, I can just cancel each other out?
So for this question,
ln2e^4 - lne^3, I can just cancel the ln and the e out? elaborate pls.
For example:
And
But if I had:
It does NOT equal 2.
So for yor example ln2e^4 - lne^3:
ln(e^3) = 3 because there's nothing else.
But ln(2e^4) has to be changed to ln(2) + ln(e^4) = ln(2) + 4.
Re: Math help (Because Carrot made me do this)
For the second example, how can you cancel the ln and e when the e and k are together?
For the first example, how can you cancel the e and the ln if the ln and k are together?They ONLY cancel each other out if there's nothing else except e and ln.
For example:
And
But if I had:
It does NOT equal 2.
So for yor example ln2e^4 - lne^3:
ln(e^3) = 3 because there's nothing else.
But ln(2e^4) has to be changed to ln(2) + ln(e^4) = ln(2) + 4.
For the second example, how can you cancel the ln and e when the e and k are together?
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,145
- Gender
- Male
- HSC
- 2010
Re: Math help (Because Carrot made me do this)
Because they're inverse functions.
Because they're inverse functions.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
You can't just hav a ln function by itself.
More specifically, (I know you don't like this math-y kind of explanation, but hopefully you will understand some part of it).
If f(x) and g(x) are inverse functions of each other, then f(g(x)) = g(f(x)) x.
So if f(x) = ln(x) and g(x) = e^x, then e^ln(x) = x and ln(e^x) = x.
Well you have to have something in the function f(x)=e^x.For the first example, how can you cancel the e and the ln if the ln and k are together?
For the second example, how can you cancel the ln and e when the e and k are together?
You can't just hav a ln function by itself.
More specifically, (I know you don't like this math-y kind of explanation, but hopefully you will understand some part of it).
If f(x) and g(x) are inverse functions of each other, then f(g(x)) = g(f(x)) x.
So if f(x) = ln(x) and g(x) = e^x, then e^ln(x) = x and ln(e^x) = x.
Re: Math help (Because Carrot made me do this)
Don't get any of what you just said. What is an inverse function? Maybe it is a good idea to **** learn my way through 3U next year since I obviously can't understand anything.Well you have to have something in the function f(x)=e^x.
You can't just hav a ln function by itself.
More specifically, (I know you don't like this math-y kind of explanation, but hopefully you will understand some part of it).
If f(x) and g(x) are inverse functions of each other, then f(g(x)) = g(f(x)) x.
So if f(x) = ln(x) and g(x) = e^x, then e^ln(x) = x and ln(e^x) = x.
Last edited by a moderator:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
And no, please don't do that. It's not too late you know.
If you're going to get tutored, may as well go 1 to 1, not classes.Don't get any of what you just said. What is an inverse function? Maybe it is a good idea to **** learn my way through 3U next year since I obviously can't understand anything.
And no, please don't do that. It's not too late you know.
Solution
BoS Revolutionary
- Joined
- Aug 3, 2012
- Messages
- 120
- Gender
- Undisclosed
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
ln(e^k) = kln(e)
Since we know ln(e) = 1 via our log laws,
ln(e^k) = k(1) = k.
For the second example, utilise your log laws:For the first example, how can you cancel the e and the ln if the ln and k are together?
For the second example, how can you cancel the ln and e when the e and k are together?
ln(e^k) = kln(e)
Since we know ln(e) = 1 via our log laws,
ln(e^k) = k(1) = k.


