scaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,604
- Gender
- Undisclosed
- HSC
- 1999
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
as they say its the fundamental theorem of calculus:View attachment 40452
how do they go from the first line to the second?
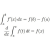
for i, b>1, meaning that arg(z1) is between pi/4 and pi/2 since when b = 1 the argument is pi/4 (tan inverse 1) and otherwise it increases.View attachment 40453
how do you do part (iii)?
also im not super confident with the rest, so i would appreciate if someone could go through them all please
To help with the drawing, Z3 lies on a circle with OZ1 as radius and O as the centre (because of the equal moduli). Z2 lies in the fourth quadrant and is inside this circle, so after extending OZ2 in both directions, the two possible locations of Z3 are the intersections of this extended line with the circle.for i, b>1, meaning that arg(z1) is between pi/4 and pi/2 since when b = 1 the argument is pi/4 (tan inverse 1) and otherwise it increases.
for z2, 0<c<1: so arg(z2) is between 0 and -pi/4 since when c = 0, argument is 0, and when c=1 the argument is -pi/4
u can just pick any points where those conditions are met basically
for ii), u need to pick z3 such that there is aline from z2 to z3 passing through the origin with same modulus of z1 that u drew, there should be two (notice that z2 modulus is less than z1, so u ahve a point in quadrant 2 and quadrant 4, just draw it and it should make more sense)
for iii), essentially it boils down to noticing that the points are collinear. In the case where z3 is in quadrant 4, k is simply -(alpha +beta), because the complex number needs to rotate z1 clockwise to have the same argument as z2, so thats just the argument of z1 + argument of z2, but negated bc clockwise rotation.
in the case where z3 is in quadrant 2; using some trig, in this case z3 is a 180 degree rotation of z2 (collinear, if that makes sense? idk how to say this), and in this case 180 = k + alpha + beta, meaning that k = 180 - alpha - beta.
i think this is correct, if someone could double check
for iii), essentially it boils down to noticing that the points are collinear. In the case where z3 is in quadrant 4, k is simply -(alpha +beta), because the complex number needs to rotate z1 clockwise to have the same argument as z2, so thats just the argument of z1 + argument of z2, but negated bc clockwise rotation.
in the case where z3 is in quadrant 2; using some trig, in this case z3 is a 180 degree rotation of z2 (collinear, if that makes sense? idk how to say this), and in this case 180 = k + alpha + beta, meaning that k = 180 - alpha - beta.
i think this is correct, if someone could double check

oh thats maybe why, bc beta represents the argument instead of the actual angleView attachment 40455
thanks, for part iii i got the same answer as you, but the solutions have this. is it possible the solutions are wrong, or, maybe is it becuase beta is actually negative?
for part i, would the angle between the positive x-axis and z2 be 'beta' OR '-beta'?
so in this case, would the answer given be correct or wrong?From the definition in the question,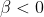
Principal Argument is the argumentfor part i, would the angle between the positive x-axis and z2 be 'beta' OR '-beta'?
like what is the difference between an argument and principal argumnet?
i think it would be correct cause beta just becomes negativeso in this case, would the answer given be correct or wrong?
so like how does this chance things?Principal Argument is the argument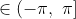
yesso like how does this chance things?
so like a normal argument of 7pi/4 would be a principal argument of -pi/4 ??
yes, basically. all it means is that in this case beta can ONLY be between -pi/4 and 0, instead of between 7pi/4 and 2pi, 15pi/4 and 4pi, etc..so like how does this chance things?
so like a normal argument of 7pi/4 would be a principal argument of -pi/4 ??
the normal argument encompasses all values, so between -pi and pi it is the same as the principal argument but otherwise it is notis the prinicple argumant ever the same as the normal argument?
if so, when is it the same?
The answers given are correct.so in this case, would the answer given be correct or wrong?
I can writeis the prinicple argumant ever the same as the normal argument?
if so, when is it the same?
