SB257426
Very Important User
I have come across some questions that are asking me to prove the general formula for a certain sequence. I do now know how to tackle these questions. Can someone please tell me how to do them?
Here is a problem from the question set that appeared:
A sequence is given by the first order recursive formula:

Prove the general formula for the sequence is:
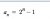
Any help will be appreciated,
Cheers
Here is a problem from the question set that appeared:
A sequence is given by the first order recursive formula:

Prove the general formula for the sequence is:
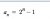
Any help will be appreciated,
Cheers
