TheOnePheeph
Active Member
- Joined
- Dec 13, 2018
- Messages
- 241
- Gender
- Male
- HSC
- 2019
My Attempt:If you have read #162, this one should not be challenging.
\sin\left(\ln x\right)dx=\frac{x\left(\ln^2x\right)\left(\sin\left(\ln x\right)-\cos\left(\ln x\right)\right)}{2}+x\left(\ln x\right)\cos\left(\ln x\right)-\frac{x\left(\sin\left(\ln x\right)+\cos\left(\ln x\right)\right)}{2}+c)
Attachments
-
633.7 KB Views: 9
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
My Attempt:If you have read #162, this one should not be challenging.
\sin\left(\ln x\right)dx=\frac{x\left(\ln^2x\right)\left(\sin\left(\ln x\right)-\cos\left(\ln x\right)\right)}{2}+x\left(\ln x\right)\cos\left(\ln x\right)-\frac{x\left(\sin\left(\ln x\right)+\cos\left(\ln x\right)\right)}{2}+c)
Was this one solved or not? The trick is quite similar.
Well then, guess I'll try it.Was this one solved or not? The trick is quite similar.
^{19}}{x^{\frac{72x-73}{3x}} + \left(\log_5 x\right)^{24}}} + \frac{1}{\sqrt{x}}\right)\left(\sqrt{x} - \sqrt[5]{\frac{x^{\frac{76x+75}{4x}} - \left(\log_3 x\right)^{19}}{x^{\frac{72x-73}{3x}} + \left(\log_5 x\right)^{24}}} + \frac{1}{\sqrt{x}}\right) \log_2\left(\frac{x}{e}\right) dx)
God,This one should lead you to a well-known tedious integral.
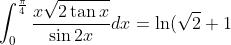+\frac{\pi}{2\sqrt{2}}-\frac{\pi}{2})
This is not challenging.
}{x^{1+\sin x}}dx=\sqrt{\frac{6}{\pi}}-\frac{2019\pi}{2})
Again, my scanner cropped a bit of the solutions, pretty much just dus and dxs. These were really good questions thoughA couple more
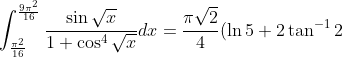)

