I hadn't heard of King's Property but a quick Google says that it is
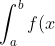 \mathrm{d} x = \int_a^b f(a+b-x) \mathrm{d}x)
You prove this using integration by substitution. The version that you use for all of these questions is:
 \mathrm{d} x = \int_{-a}^a f(-x) \mathrm{d} x. )
For the first one, let I equal to the value of the definite integral. By King's Property, you can say that
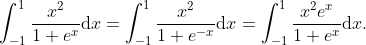
You can then add two of I together to get:

For the second one, you apply King's property to show that
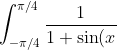} \mathrm{d}x = \int_{-\pi/4}^{\pi/4} \frac{1}{1+\sin(-x)} \mathrm{d}x = \int_{-\pi/4}^{\pi/4} \frac{1}{1-\sin(x)} \mathrm{d}x.)
If J is the value of the definite integral, then you can say that
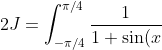} \mathrm{d}x + \int_{-\pi/4}^{\pi/4} \frac{1}{1-\sin(x)} \mathrm{d}x = \int_{-\pi/4}^{\pi/4} \frac{2}{1-\sin^2(x)} \mathrm{d}x = \int_{-\pi/4}^{\pi/4} 2 \sec^2 (x) \mathrm{d}x = 2 \left[ \tan(x)\right]_{-\pi/4}^{\pi/4} = 4 \Rightarrow J = 2.)
For the last one, it's very similar so I'll skip some steps. If K is the value of the definite integral, then
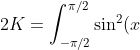 \mathrm{d} x = \frac{\pi}{2} \Rightarrow K = \frac{\pi}{4}.)