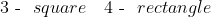==================================
|---------- x --------- ||-------(7-x)------|
A piece of wire is shown above cut into 2 pieces of lengths x and 7-x, since the wire is 7 metres long.
Now lets take x to be the wire cut into a square.
In such a square the perimeter must be x, hence since all sides are equal, each side length of our square is x/4
Hence the area of our square is (x/4)^2
Looking at the rectangle, first leave the piece of wire alone, and consider a rectangle where the length is three times the width.
|-----------------------|
|................................|
|................................|
|-----------------------|
Let the dotted length be 3y, and the dashed width be y. (IGNORE the dots in the middle)
The perimeter of this will be: 3y + 3y + y + y = 7 - x
Hence it must follow that:
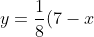 )
Now, we have constructed the shapes and now we need to find the areas of them:
^2 + 3y^2 )
Where A is the area
Lets sub in our x from before, it follows that
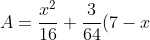^2 )
We need to find the minimum x
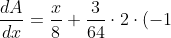 \cdot (7-x) )
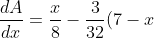 )
Now we equate this to zero and solve for x
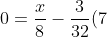 + \frac{3}{32}x )

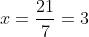
Finding the second derivative to text our answers

Therefore the result we found is a minimum, hence the length of the two parts are: