-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
The official solutions/feedback for this question is as follows:
Part (i) of this question is a very straightforward single-pulley scenario, with the tension in the string equal throughout its length, which is constant, and the accelerations of the particles equal (relative to the string). Using Newton’s Second Law for each particle gives the acceleration (as shown) and the tension in the string given by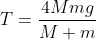
In the second part of the question, we apply exactly the same assumptions and principles in exactly the same way, but there is a complication imposed now by the relative accelerations of the two particles on the P1 pulley system. If we assume that the P1 system has the “same” acceleration as the particle on the LHS of P, then (assuming that the m1 particle accelerates downwards within this sub-system) the two particles on the RHS have accelerations b – a2 and b + a2 respectively. Also, since P1 is taken to have zero mass, the tension in the main string is twice the tension in the sub-system. Without this set-up, the following working is most unlikely to be meaningful in any mark-scoring capacity. N2L applied several times, for the different particles, then leads to a set of equations that gives the second printed answer.
With two given answers, the very final part of the question can be done as a “stand alone” piece of work. Notice, however, that this is an if and only if proof and thus requires either two separate arguments or one in which every step is reversible. In point of fact, it transpires that a1 = a2 if and only if (m1 – m2) 2 = 0, which is equivalent to m1 = m2.
I hope this helps!
Part (i) of this question is a very straightforward single-pulley scenario, with the tension in the string equal throughout its length, which is constant, and the accelerations of the particles equal (relative to the string). Using Newton’s Second Law for each particle gives the acceleration (as shown) and the tension in the string given by
In the second part of the question, we apply exactly the same assumptions and principles in exactly the same way, but there is a complication imposed now by the relative accelerations of the two particles on the P1 pulley system. If we assume that the P1 system has the “same” acceleration as the particle on the LHS of P, then (assuming that the m1 particle accelerates downwards within this sub-system) the two particles on the RHS have accelerations b – a2 and b + a2 respectively. Also, since P1 is taken to have zero mass, the tension in the main string is twice the tension in the sub-system. Without this set-up, the following working is most unlikely to be meaningful in any mark-scoring capacity. N2L applied several times, for the different particles, then leads to a set of equations that gives the second printed answer.
With two given answers, the very final part of the question can be done as a “stand alone” piece of work. Notice, however, that this is an if and only if proof and thus requires either two separate arguments or one in which every step is reversible. In point of fact, it transpires that a1 = a2 if and only if (m1 – m2) 2 = 0, which is equivalent to m1 = m2.
I hope this helps!
lol where's this q from?
nsb 2021 i think
this one's formatted tho lol.
this explanation involved newtons second law and other physics concepts so i think its safe to think the original question is not assessable. The first part is, not the second.The official solutions/feedback for this question is as follows:
Part (i) of this question is a very straightforward single-pulley scenario, with the tension in the string equal throughout its length, which is constant, and the accelerations of the particles equal (relative to the string). Using Newton’s Second Law for each particle gives the acceleration (as shown) and the tension in the string given by
In the second part of the question, we apply exactly the same assumptions and principles in exactly the same way, but there is a complication imposed now by the relative accelerations of the two particles on the P1 pulley system. If we assume that the P1 system has the “same” acceleration as the particle on the LHS of P, then (assuming that the m1 particle accelerates downwards within this sub-system) the two particles on the RHS have accelerations b – a2 and b + a2 respectively. Also, since P1 is taken to have zero mass, the tension in the main string is twice the tension in the sub-system. Without this set-up, the following working is most unlikely to be meaningful in any mark-scoring capacity. N2L applied several times, for the different particles, then leads to a set of equations that gives the second printed answer.
With two given answers, the very final part of the question can be done as a “stand alone” piece of work. Notice, however, that this is an if and only if proof and thus requires either two separate arguments or one in which every step is reversible. In point of fact, it transpires that a1 = a2 if and only if (m1 – m2) 2 = 0, which is equivalent to m1 = m2.
I hope this helps!
The North Sydney Boys High School 2021 paper's version of this question is slightly different. OP's question is from a STEP paper. STEP papers are developed by the University of Cambridge and are designed to test candidates on questions that are similar in style to undergraduate mathematics.
nsbhs 2021 took the step question then removed the scaffolding lmfaoThe North Sydney Boys High School 2021 paper's version of this question is slightly different. OP's question is from a STEP paper. STEP papers are developed by the University of Cambridge and are designed to test candidates on questions that are similar in style to undergraduate mathematics.