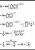Someone gives me this solution using Stolz Cesaro as well but i don't really get it. Can you please write down a detailed solution for me? ThanksHere is another method using the Stolz–Cesàro theorem. It starts the same as the first method but then goes in a completely different direction, nevertheless ending up at the same answer.
Method 3.
^\frac{1}{n(n+1)}=e^\frac{1}{2}=\sqrt e)
Attachments
-
207 KB Views: 7