-
Looking for HSC notes and resources? Check out our Notes & Resources page
Can't you just prove this by contradiction?
^n - 2^n - 3^n \\ &= \binom{n}{0} 2^n + \binom{n}{1}2^{n-1} \times 3 + \binom{n}{2}2^{n-1} \times 3^2 + ... + \binom{n}{n-1}2^1 \times 3^{n - 1} + \binom{n}{n} 3^n - 2^n - 3^n \qquad \text{provided $n \in \mathbb{Z}$ and $n > 1$} \\ &= 2^n + \binom{n}{1}2^{n-1} \times 3 + \binom{n}{2}2^{n-1} \times 3^2 + ... + \binom{n}{n-1}2^1 \times 3^{n - 1} + 3^n - 2^n - 3^n \qquad \text{as $\binom{n}{0} = \binom{n}{n} = 1$} \\ &= \binom{n}{1}2^{n-1} \times 3 + \binom{n}{2}2^{n-1} \times 3^2 + ... + \binom{n}{n-1}2^1 \times 3^{n - 1} \\ &> 0 \qquad \text{as every term in this sum is positive} \\ &\neq \text{RHS} \end{align*})
So, we have a contradiction provided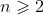 , and so the assumption / supposition is false and the theorem is true.
, and so the assumption / supposition is false and the theorem is true.
Hence,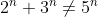 for any integer
for any integer 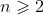 . The statement
. The statement 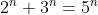 is obviously true for
is obviously true for 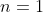
So, we have a contradiction provided
Hence,
I wonder what they would make of a proof that invoked Fermat's Last Theorem and noted that this was proven by Andrew Wiles a few years ago, pointing at that if there are no solutions in positive integers  ,
,  , and
, and  for the statement
for the statement 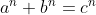 for any integer
for any integer 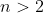 , and then pointing out that with
, and then pointing out that with 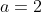 ,
, 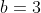 , and
, and 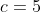 , the
, the 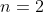 case is also false as
case is also false as 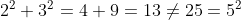 . Thus
. Thus 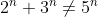 for all integers
for all integers 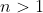 .
.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
Will there be anybody here showing Sydney Morning Herald how to do Q16 this year?
I am curious. There will always be those boomers who say so what, skills in the real world are more important than a little mathematical equation. Typical boomer talk from the Sydney Morning herald. They never learn.
I am curious. There will always be those boomers who say so what, skills in the real world are more important than a little mathematical equation. Typical boomer talk from the Sydney Morning herald. They never learn.
Paradoxica
-insert title here-
For a non-binomial method, divide both sides by 3^n to obtain
(2/3)^n + 1 = (5/3)^n
The left hand side has a base smaller than 1 and is a strictly decreasing function of n, and the right hand side is likewise strictly increasing.
Thus, there can only be at most one solution, which is obviously n=1. Hence, the two expressions are unequal for n>1
(2/3)^n + 1 = (5/3)^n
The left hand side has a base smaller than 1 and is a strictly decreasing function of n, and the right hand side is likewise strictly increasing.
Thus, there can only be at most one solution, which is obviously n=1. Hence, the two expressions are unequal for n>1
Paradoxica
-insert title here-
1995 is more than a few years....I wonder what they would make of a proof that invoked Fermat's Last Theorem and noted that this was proven by Andrew Wiles a few years ago, pointing at that if there are no solutions in positive integers,
, and
for the statement
for any integer
, and then pointing out that with
,
, and
, the
case is also false as
. Thus
for all integers
.
I feel old1995 is more than a few years....
icycledough
Well-Known Member
- Joined
- Aug 5, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2020
I believe this was the exam.can anyone find the ext 2 paper?
Attachments
-
5.6 MB Views: 42
michealhunter@school
New Member
- Joined
- Aug 26, 2020
- Messages
- 5
- Gender
- Male
- HSC
- 2021
I let the LHS and RHS be different functions then I differeniated both functions and showed that 5^x increases faster than 2^x
+ 3^x after x =1. Dunno if its worth full marks but it worked out for me.
+ 3^x after x =1. Dunno if its worth full marks but it worked out for me.
icycledough
Well-Known Member
- Joined
- Aug 5, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2020
That does seem like a valid way of going about it (I think there must be various ways to go about it, so as long as you could set your answer out and it made sense in a chronological manner, then it should be fine). I guess with the topics of proofs, what makes it nice is the level of flexibility with regards to what method you can use for an individual question.I let the LHS and RHS be different functions then I differeniated both functions and showed that 5^x increases faster than 2^x
+ 3^x after x =1. Dunno if its worth full marks but it worked out for me.

