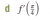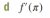-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
How do you solve these questions. As i keep getting them wrong (1 Viewer)
- Thread starter Dane Red
- Start date
synthesisFR
afterhscivemostlybeentrollingdonttakeitsrsly
what are you struggling with? understanding chain rule or something else?
Average Boreduser
Rising Renewal
is this prelim or hsc 2U?
synthesisFR
afterhscivemostlybeentrollingdonttakeitsrsly
diff trig is hsc content
mmmmmmmmaaaaaaa
Well-Known Member
- Joined
- Jun 11, 2021
- Messages
- 1,412
- Gender
- Male
- HSC
- 2022
What exactly are you struggling with in these questions? Which step of the question do you get stuck on
Theorems
sin x(d/dx)= cos x
cos x(d/dx) = -sin x
-sin x(d/dx) = -cos x
-cos x(d/dx) = sin x
The proof of these theorems is outside the scope of high school however nothing will stop you from applying the theorem.
Other than that question are fairly straightforward, so you may need to apply product rule or chain rule
You could do this but it does not demonstrate understanding of chain rule.Just remember these:
y = sin [ f(x) ]
y' = f'(x) x cos [ f(x) ]
y = cos [ f(x) ]
y' = f'(x) x -sin [ f(x) ]
y = tan [ f(x) ]
y' = f'(x) x sec^2 [ f(x) ]
Let's apply this to the question above:
y = sin [ 1/4x + pi/2 ]
So f(x) = 1/4x + pi/2
f'(x) = 1/4
Therefore y' = 1/4 x cos [ 1/4x + pi/2 ]
But the question is asking for y'(pi)
So in place of x, we now substitute x = pi
Doing this we get y'(pi) = 1/4 x cos [ 1/4(pi) + pi/2 ] = ________
You can take it step by step until you reach your answer, don't get overwhelmed
As a side note you should use * for multiplication has "x" can be confused with the variable "x".
The problem is that the answer i get is different to the answer in the text book