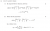For 7bi, my method is slightly different to the other posted, but plug x=p/q into the polynomial equation. Doing so and rearranging gives the result:
 )
This means that, since all the numbers present are integers, p divides bq^3. But p and q are coprime (p does not divide q) meaning this can only happen if p divides b. A similar argument can be made rearranging for the ap^3 term. This is essentially proving a case of the rational root theorem, which is for some reason not explicitly taught in 4u.
For 8biii), if we plug r=p/q into the expression, we get:

Now we have two cases to consider. If aq = -bp, then the expression clearly equals 0. Otherwise, however, we know that a,q,b and p are integers, so as long as the expression aq+bp does not equal 0, it will also be an integer. Since all non zero integers have an absolute value greater than or equal to 1:

This means that the given expression is greater than or equal to 1/q.
For 8b iv), we simply consider parts 1 and 2 to show that:

Note, we have assume e=p/q, for coprime p and q, so let a=3q.

But this contradicts the result proved in part iii for rational numbers. Therefore, e must be irrational.